One often hears pundits proclaim "Modelers don't clean up when rolling off the volume knob". While this may be true of some products we actually test and compare this to our reference amps. We measure the THD and output volume at different stimulus levels to ensure that the response is the same.
The reason for this myth stems from acoustic feedback. Real amps are LOUD. Modelers are usually played at much lower volumes.
Consider the following diagram:
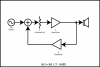
This is a block diagram of a model of what happens when playing a guitar with a speaker. Vg is the signal generator (your guitar). Sound waves from the speaker are fed back to your guitar and add to that signal. This signal is then attenuated by the the volume pot, k. The signal is amplified by the amp gain, A. Some portion of that signal is fed back, B.
The formula for a closed loop system like this is Acl = kA / (1 - kAB), where Acl denotes the closed loop gain. The open loop gain is given by Aol = kA.
Let's consider some examples.
In the first example let's assume the amp gain, A = 10, the volume knob is wide open, k = 1 and a mere 2% of the signal is fed back, B = 0.02. Using our formula we get:
Acl = 10 / (1 - 10 * 0.02) = 12.5.
The open loop gain is Aol = 10.
That tiny 2% of feedback has INCREASED the effective gain by 25% (!!!). If the amp is approaching distortion then it will get more distorted.
Now consider what happens if we roll of the volume knob a bit. Let's assume everything else is the same but we set our Log10A volume pot to halfway which means k = 0.1. Now we get:
Acl = 0.1 * 10 / (1 - 0.1 * 10 * 0.02) = 1.02
and Aol = 1
Rolling our volume knob to halfway now only gives a paltry 2% of gain increase for the same amount of acoustic feedback. So when the volume knob is wide open the amp has effectively almost 25% more gain than when rolled off halfway!
Now let's look at what happens when we lower the amount of feedback which would occur if we turned down the volume of our speaker. Let's leave everything the same but reduce our feedback to 1%.
Our first example with the volume pot wide open now becomes:
Acl = 10 / (1 - 10 * 0.01) = 11.1
Aol = 10
And our second example becomes:
Acl = 1.01
Aol = 1
So we see that the closed-loop gain is highly dependent upon the speaker volume. Simply reducing the speaker volume by 6dB lowers the effective gain increase considerably.
When playing with a loud amp the positive feedback from the speaker into the guitar effectively increases the gain of the amp when the volume control is wide open. As you roll the volume control off the amount of gain increase is lower. This gives the ILLUSION that the amp cleans up more when you roll of the volume but it's not the amp that is cleaning up, the signal into the amp is lowered more than if there were no feedback.
When using a modeler people almost always have the volume lower because amps are too loud. Lowering the volume reduces the feedback which in turn lowers the gain enhancement. To compensate people raise the gain of the model but now when you roll off the volume it doesn't clean up as much because the gain is higher. IOW, to compensate for the reduced feedback the user increases the gain, say, 25% to get the same effective gain as the loud amp but when rolling off the volume the amp gain is still 25% higher so it doesn't clean up as much.
P.S.
An interesting result occurs if we let B = 0.1:
Acl = 10 / (1 - 10 * 0.1) = 10 / 0 = infinity.
This is what happens for controlled feedback. The closed loop gain approaches infinity and the loop becomes unstable and oscillates. That's why controlled feedback is easier to obtain at higher volumes, the feedback coefficient is greater. Another way is to move closer to the speaker. Since sound pressure is inversely proportional to the square of the distance moving 50% closer results in four times the feedback!
The reason for this myth stems from acoustic feedback. Real amps are LOUD. Modelers are usually played at much lower volumes.
Consider the following diagram:

This is a block diagram of a model of what happens when playing a guitar with a speaker. Vg is the signal generator (your guitar). Sound waves from the speaker are fed back to your guitar and add to that signal. This signal is then attenuated by the the volume pot, k. The signal is amplified by the amp gain, A. Some portion of that signal is fed back, B.
The formula for a closed loop system like this is Acl = kA / (1 - kAB), where Acl denotes the closed loop gain. The open loop gain is given by Aol = kA.
Let's consider some examples.
In the first example let's assume the amp gain, A = 10, the volume knob is wide open, k = 1 and a mere 2% of the signal is fed back, B = 0.02. Using our formula we get:
Acl = 10 / (1 - 10 * 0.02) = 12.5.
The open loop gain is Aol = 10.
That tiny 2% of feedback has INCREASED the effective gain by 25% (!!!). If the amp is approaching distortion then it will get more distorted.
Now consider what happens if we roll of the volume knob a bit. Let's assume everything else is the same but we set our Log10A volume pot to halfway which means k = 0.1. Now we get:
Acl = 0.1 * 10 / (1 - 0.1 * 10 * 0.02) = 1.02
and Aol = 1
Rolling our volume knob to halfway now only gives a paltry 2% of gain increase for the same amount of acoustic feedback. So when the volume knob is wide open the amp has effectively almost 25% more gain than when rolled off halfway!
Now let's look at what happens when we lower the amount of feedback which would occur if we turned down the volume of our speaker. Let's leave everything the same but reduce our feedback to 1%.
Our first example with the volume pot wide open now becomes:
Acl = 10 / (1 - 10 * 0.01) = 11.1
Aol = 10
And our second example becomes:
Acl = 1.01
Aol = 1
So we see that the closed-loop gain is highly dependent upon the speaker volume. Simply reducing the speaker volume by 6dB lowers the effective gain increase considerably.
When playing with a loud amp the positive feedback from the speaker into the guitar effectively increases the gain of the amp when the volume control is wide open. As you roll the volume control off the amount of gain increase is lower. This gives the ILLUSION that the amp cleans up more when you roll of the volume but it's not the amp that is cleaning up, the signal into the amp is lowered more than if there were no feedback.
When using a modeler people almost always have the volume lower because amps are too loud. Lowering the volume reduces the feedback which in turn lowers the gain enhancement. To compensate people raise the gain of the model but now when you roll off the volume it doesn't clean up as much because the gain is higher. IOW, to compensate for the reduced feedback the user increases the gain, say, 25% to get the same effective gain as the loud amp but when rolling off the volume the amp gain is still 25% higher so it doesn't clean up as much.
P.S.
An interesting result occurs if we let B = 0.1:
Acl = 10 / (1 - 10 * 0.1) = 10 / 0 = infinity.
This is what happens for controlled feedback. The closed loop gain approaches infinity and the loop becomes unstable and oscillates. That's why controlled feedback is easier to obtain at higher volumes, the feedback coefficient is greater. Another way is to move closer to the speaker. Since sound pressure is inversely proportional to the square of the distance moving 50% closer results in four times the feedback!
Last edited:
